The content below is presented in the following videos:
music
Let's listen to a scale:
That was a scale derived from overtones of the harmonic series, and if it sounded a little out to you, maybe this one will sound more familiar:
Here's another one:
Here's a really wacky one:
And here is, without a doubt, the most common scale in modern times:
Ok, so there are all kinds of scales. And all of those scales we just heard (except for maybe the wacky one) could make a claim to being the "most natural". But there's no single most natural scale, of course. In fact, each method of constructing a scale necessitates some compromise in terms of harmony, or being "in tune", because, well, because math! As we'll see. Mathematics can shed all kinds of light on all sorts of questions and problems that arise when we try and build scales, and math can help us appreciate the rich variety of scales. And here's my favourite quote, from Georg Cantor: "the essence of mathematics lies in its freedom", so once you understand the mathematics, you can create your own scales.
So we're going to talk about scales, which you can think of as choosing a bunch of notes, and tunings, which you can think of as choosing how, exactly, to tune each of those notes. The difference between the two isn't always clear cut, to be sure.
And I don't want to assume much familiarity with music theory, but this whole exploration will go a lot smoother if we can use some modern-day terminology.
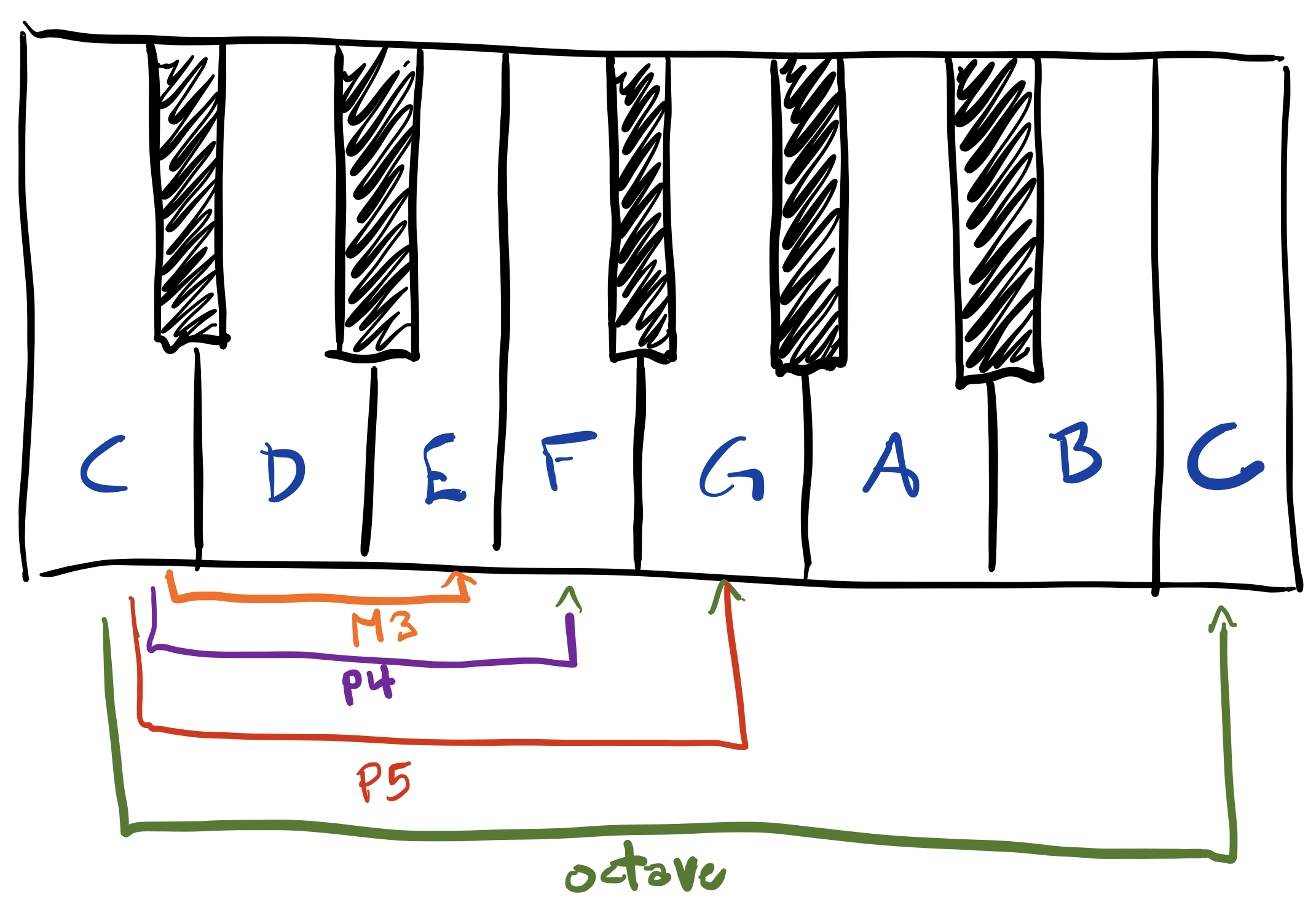
The seven white keys of a piano constitute what's now called a C-major scale; C is called the root note. The eighth, rightmost white key is also a C. The white and black keys together constitute the 12-note chromatic scale. The interval from one key to the next is called a semitone.
Modern pianos are equally tempered, so the ratio of one frequency to one a semitone below is \(2^{1/12}\); we'll learn more about this in a bit.
Referring to the picture, the green interval is called a perfect octave, and sounds like this:
The red interval is called a perfect fifth and sounds like
The purple interval is called a perfect fourth and sounds like
The orange interval , four semitones, is called a major third.
The interval from E to G is also a third, but it's called a minor third because it's only 3 semitones.
We also have intervals of major 2nd (2 semitones), major sixth (9 semitones), major seventh (11 semitones), etc.
When talking about scales and tunings, there's a useful unit called a "cent". A (equally-tempered) semitone is equal to 100 cents. Since a semitone corresponds to a ratio of \(2^{1/12}\), a single cent corresponds to a ratio of \(2^{1/1200}\). For most people, the threshold for differentiation of pitches seems to be about 5 cents; most people can perceive that these two tones are different:
but can't perceive that these two are different
This is an important point that will come up again later: we can't perceive really small changes in pitch.
Ok. Why seven notes in the major scale? Why is the eighth white key also called C? Why 12 notes in the chromatic scale? Why not 13, or 9, or 21?
Why does the major scale have a whole-whole-half-whole-whole-whole-half pattern? Sometimes these questions are answered with a vague, well, because history, or because culture, or because the ear. But mathematics has a heck of a lot more to say about it. Of course it's true that culture and history play the dominant role in determining what sounds "good" or "interesting" to human ears, but math certainly sheds significant light on why scales are what they are.
fourier
Let's talk about sound for a minute.
When an object like a drum head or a tight string vibrates, it moves the air around it.
Say the black lines represent a vibrating object. As the object moves to the right, the air next to it compresses into a small high pressure region.

This high pressure region will then push against the relatively low pressure region next to it, and a chain reaction ensues.
So the vibrating object causes little pockets of air to oscillate, and the variations in the air pressure to propagate away from the source; this is called a sound wave.
You can see that the air pressure of a region goes up and down, as represented by a dot. If we plot the change in air pressure over time, we get a sine wave.
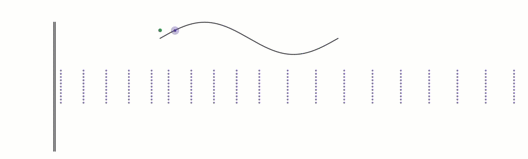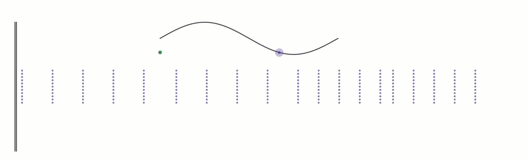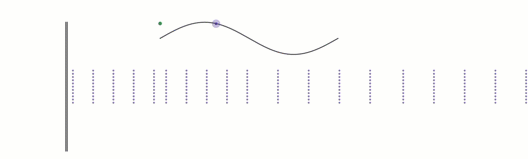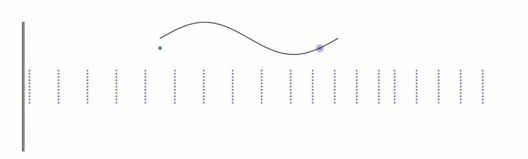
How fast the object vibrates will determine how fast these little pockets of air move back and forth.
If, for example, they go back and forth 130 times in one second, we would say the sound wave has a frequency of 130 Hz. The wavelength is the distance from one little pocket of air to the next, and wavelength and frequency are inversely proportional, so for example, doubling the frequency halves the wavelength.
If the frequency of the wave is somewhere between 20 Hz and 15 000 Hz, and there's a functioning human ear around, these tiny disturbances in the air pressure will disturb the inner mechanisms of the ear, which in turn will send a signal to the brain that is interpreted as sound.
Here's the Desmos worksheet:
If the frequency of a sound wave is doubled, it is exceedingly common for the human brain to interpret that new frequency as "the same note".
The invterval from the lower to the higher, doubled frequency is nowadays called an octave (yes, octa for eight, but that naming has nothing to do with doubling frequency, and everything to do will scale construction, as we'll see later).
It has long been thought that this perception of octaves is due to the biology of the human ear, though recent ethnomusicological studies cast some doubt on this. It may have more to do with the kinds of instruments we have lone played as a species: instruments made of cylindrical tubes, or stretched strings or membranes (see, for instance, David Benson's book).
For example, a tight string will oscillate something like this
 We'll call this tone the fundamental.
We'll call this tone the fundamental.
But it will also oscillate a bit like this, although to a lesser extent
 This is called the first overtone.
Note that the wavelength is halved, so the frequency is doubled, so this is perceived as an octave above the fundamental.
This is called the first overtone.
Note that the wavelength is halved, so the frequency is doubled, so this is perceived as an octave above the fundamental.
But there's more: the string also oscillates a bit like this:
 and this:
and this:

These are called "overtones", and the sequence of higher overtones is called the "harmonic series". If the fundamental is 260 Hz, then here's what these pitches (the fundamental and first four overtones) sound like in sequence:
The actual motion of the string will be some linear combination of these sine waves, and so the sound produced will be a combination of the fundamental tone, and many, many overtones.

Some overtones will be louder than others, though none will be as loud as the fundamental, and exactly how loud the many overtones are depends on where the string is plucked, what it's made of, and what the endpoints are attached to.
A similar thing happens for sound produced in cylindrical tubes (e.g. a flute or clarinet), or, in a more sophsticated way, by vibrating membranes (almost always circular).
In fact these overtones are a very large part of what differentiate a pitch played on a piano and that same pitch played on a guitar, or violin, or saxophone, etc.
Here's the Desmos worksheet:
And here is a "Fourier series" applet that allows you to experiment with adding in overtones, in varying amounts, and observing (and hearing!) the difference in the tone.
Let's use several of the first overtones from the harmonic series to try to create a scale. We'll take advantage of the fact that our ears perceive doubling or halving a frequency as producing the same note in a different octave. That is, for each overtone, let's halve it as many times as necessary for it to lie between 260 and 520Hz. So with a fundamental of 260 Hz, the second harmonic (first overtone) is 520 Hz, with a ratio of 2:1 to the fundamental. The third harmonic (second overtone) is 780Hz, with a ratio of 3:1 to the fundamental, or 3:2 to the second harmonic. Rescaled, we get 780/2 = 390Hz. The fourth harmonic (third overtone) is 1040Hz, with a ratio of 4:1 to the fundamental, or 4:3 to the third harmonic. Rescaled, we get 1040/2 = 520Hz. The fifth harmonic (fourth overtone) is 1300Hz, with a ratio of 5:1 to the fundamental, or 5:4 to the fourth harmonic. Rescaled, we get 1300/4 = 325Hz. The sixth harmonic (fifth overtone) is 1560Hz, with a ratio of 6:1 to the fundamental, or 6:5 to the fifth harmonic. Rescaled, we get 1560/4 = 390Hz. The seventh harmonic (sixth overtone) is 1820Hz, with a ratio of 7:1 to the fundamental, or 7:6 to the sixth harmonic. Rescaled, we get 1820/4 = 445Hz.

Let's see what we have so far, by putting these tones in order.
This is the same scale we played at the start of the video. If we keep going until we get two more distinct tones, we'll get
That one sounds a little weirder. We could keep going, of course, re-scaling higher and higher harmonics and slotting them into the scale, and there's no particularly obvious place to stop.
Because these overtones are produced by so many instruments that we, as a species, have played for millennia, we generally perceive them as being very harmonious. Notice how simple these ratios are, and how they start with small numbers, gradually getting larger. And the smaller the numbers in the ratio, in particular the smaller the denominator, the more harmonious they sound to us. So we can take "more harmonious" to mean precisely "occurring earlier in the harmonic series".
So let's use these harmonious intervals to explore another way to construct a scale. Two notes sounding in perfect unison is the most harmonious, an octave apart (fundamental and second harmonic) is the next harmonious, and fundamental and third harmonic, with a ratio of 3:2, is the next harmonious. An interval where the the higher frequency is 1.5 times the lower is called a "perfect fifth", although that naming, much like octave, will only make sense later. We'll start with a fundamental of 260 Hz again, and multiply by 3/2 to obtain a second tone. Then we'll multiply that frequency by 3/2, and rescale (divide by 2) so that it sits between 260 and 520 Hz. Then we'll multiply that third frequency by 3/2, rescale, and so on. We can call this process "stacking fifths".
If we perform this procedure five times, we get these tones, in order.
This probably sounds familiar; it's what's now called the major pentatonic scale , and is absolutely one of the most common scales. A great many nursery rhymes, folk songs, pop songs, have melodies that involve only the pentatonic scale.
Let's keep going to obtain a couple more distinct tones. We get this.
Now that, that's not the major scale, although it's close. For those of you who know some music theory this is a Lydian scale because of the raised fourth.
Let's keep going. We'll keep going until, well, how will we know how to stop? Will we ever, by stacking fifths (successively multiplying by 3/2), wind up some perfect octaves up from the fundamental? That is, is there some power of 3/2 that will give some power of 2? Well, let's suppose there are; that there's some integer \(k\), and some integer \(m\), with \((3/2)^k = 2^m\) (this would mean stacking \(k\) fifths would give \(m\) octaves). Then, rearranging, we'd have \(3^k = 2^m2^k = 2^{m+k}\). But the number on the left is odd, and the number on the left is even, so it's not possible for a power of 3/2 to equal some power of 2. In the current context, that means that we'll never, by stacking fifths, wind up some number of perfect octaves above the fundamental. The so-called circle of fifths never closes.
If we continue stacking fifths, at the twelfth iteration we'll obtain \(3^{12}/2^{19}\), is approximately 1.01364, which is very close to one. The two frequencies 260 and \(260*1.01364 = 263.54\) are really quite close. In modern terms, they differ by about 23 cents, which is certainly perceptible; this interval of 23 cents is called a Pythagorean comma.
Because we've almost-but-not-quite come full circle, any iterations of our procedure from this point on will produce tones which are quite close to tones we've already obtained. This is one explanation for why the chromatic scale has 12-tones.
Let's adjust our procedure just a little. Instead of only going up from the fundamental, let's also go down. By going up, we'll obtain the tones we already have; by going down we'll obtain some new ones. To go down from the fundamental of 260 Hz, we need a frequency F such that the ratio of 260 to F is 3:2; that is, \(260 = (3/2)F\), or \(F = (2/3)260 \approx 173.3\), and then re-scale, multiplying by two to get a frequency between 260 and 520: 346.6. Continuing in this way, we'll get twelve distinct tones before we start to almost repeat ourselves.
Let's look at the two lists of frequencies in increasing order, along the with the ratio each frequency makes with the fundamental.
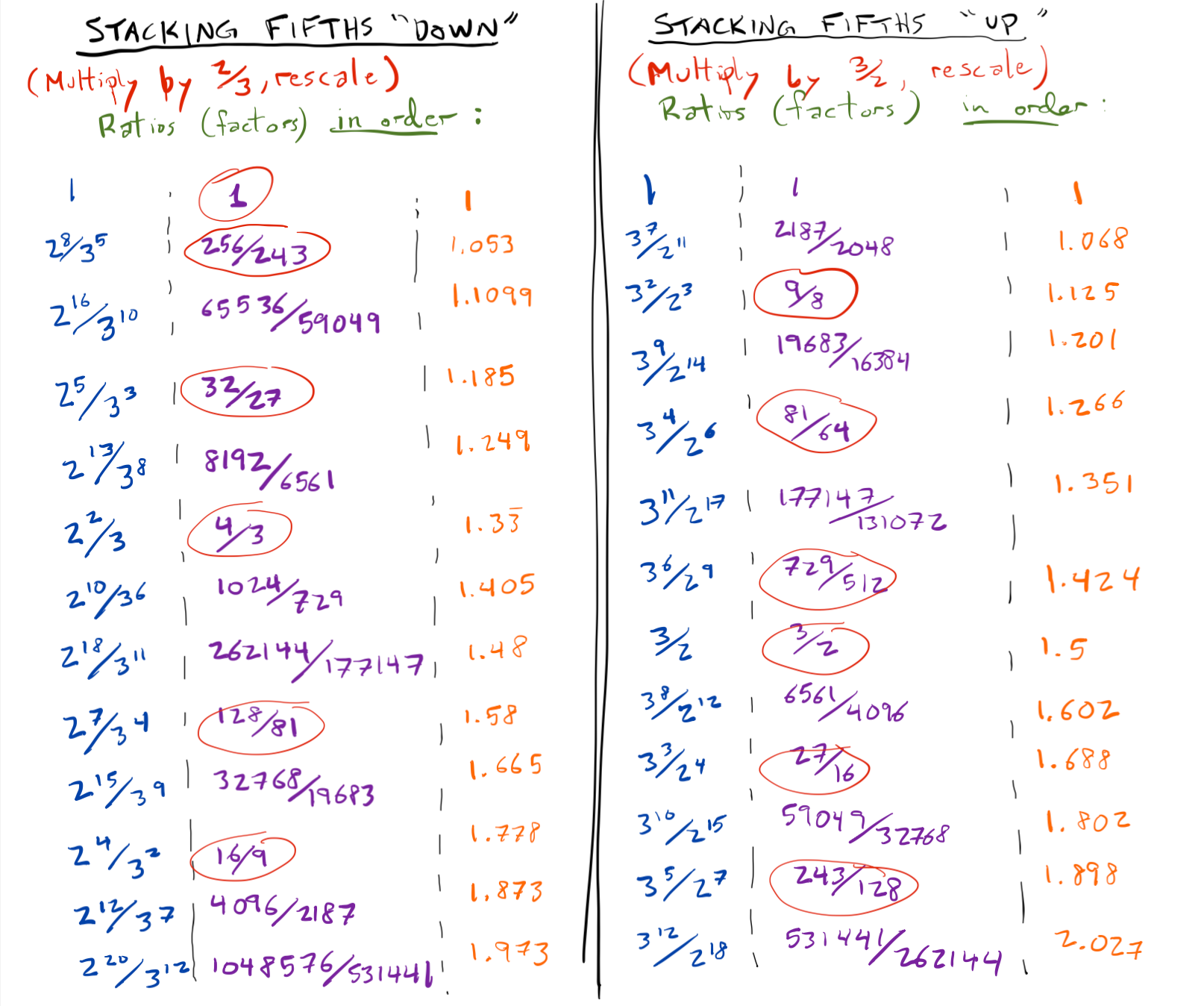 Some of these are quite close.
Our experience with the harmonic series seems to suggest that ratios with lower denominators are more harmonious; reality is a bit more subtle than that, but that did and does serve as a guiding principle in tuning, so let's choose the ratios with lower denominators.
Some of these are quite close.
Our experience with the harmonic series seems to suggest that ratios with lower denominators are more harmonious; reality is a bit more subtle than that, but that did and does serve as a guiding principle in tuning, so let's choose the ratios with lower denominators.
The resulting scale is called Pythagorean tuning, and dominated Western music for centuries. It is also called 3-limit tuning, because every pitch is obtained from the fundamental by multiplying only by powers of 2 or 3. A piano tuned according to Pythagorean tuning will mostly sound very nice, but some intervals will sound very harmonious, while others don't. Any Pythagorean tuning will result in a so-called "wolf interval", and we can calculate the ratio of these pitches to be \((1+256/243)/(729/512) \approx 1.44\), which is quite far from 1.5. Pythagorean tuning, relative to some fundamental frequency, sounds beautiful as long as the music doesn't deviate too far from the intervals that are harmonious to that fundamental, and especially avoids any wolf intervals.
In particular, let's note how the ratio of 81/64, which was obtained by stacking four fifths up, corresponds to what is now called an interval of a major third, and that 81/64 is close but noticeably sharper than the ratio 5/4 that appears early in the harmonic series. In fact the ratio between these two major thirds is \((81/64)/(5/4) = 81/80\), approximately 21.5 cents, which is called a syntonic comma. Here are the intervals in Pythagorean tuning and in the harmonic series tuning: Due to the sharpness of the major third in Pythagorean tuning, for a long time composers shied away from this less harmonious interval; the intervals of the fifth, fourth, and octave reigned supreme through most of the Middle Ages.
But maybe there's a way to refine our pitches to include the ratio of 5:4. Here's one way: if stacking four fifths result in the ratio 81:64, which is a syntonic comma sharp, if we shave off a little from each perfect fifth, that is, we temper each fifth, by one quarter of a syntonic comma, or about 5.4 cents, then stacking four of these will give a ratio of 5:4! So fifths are obtained by multiplying frequencies not by a factor of \(3/2\), but rather by \((80/81)^{1/4}(3/2) \approx 1.49535\). This method of tuning was called meantone temperament, which rose to prominence in western music in the 16th century. Remember how the threshold of differentiation of pitch for most humans seems to be about 5 cents? Meantone temperament compromises the fifths, by about 5 cents, for the benefit of the thirds.
These small changes may seem trifling and insignificant, but they had a huge impact on the creative output of composers. Intervals of a major third began to feature much more significantly, which opened the floodgates to all sorts of sophisticated harmonic ideas.
numbertheory
A different approach is to the leave the perfect fifths, the ratio 3:2, intact, and simply include the ratio 5:4 in our procedure to build a scale.
So we allow ourselves to stack fifths and thirds; this will result in a so-called 5-limit tuning, because every pitch will be obtained from the fundamental by multiplying only by powers of 2 or 3 or 5.
I won't go through all the details in the way that I did for Pythagorean tuning, but I'll mention that in deriving Pythagorean tuning we could go up or down from the fundamental, obtaining some very similar pitches, and then we had a choice to make.
The same thing happens in 5-limit tuning, and it turns out there are a few choices to make.
You might wonder if there are 7-limit tunings, 11-limit tunings, etc; indeed there are, though I won't talk about them here.
With any tuning based on these simple ratios, though, there will be disharmonious intervals, because stacking harmonious intervals does not necessarily result in all harmonious intervals. This may not be an issue, for example if a piece of music avoids the dissonant intervals. Or, for instruments that can produce microtones, like fretless stringed instruments, trombones, or voices, skilled performers may adjust the intonation of notes on the fly within a piece of music. But for a keyboard instrument, it's impossible to tune it in such a way that all intervals are harmonious.
Thus, compromises must be made. One way of compromising, which has come to dominate music theory, at least in the West, is to divide the octave up into an equal number of tones. In this tuning, we decide that the ratio between each and every semitone is to be the same, let's call it \(r\), and if there are to be 12 tones in an octave, this means \(r^{12} = 2\), so \(r = 2^{1/12}\). If a semitone consists of 100 cents, then \(2^{1/12} = c^{100}\), so 1 cent corresponds to a factor of \(2^{1/1200}\). We can now verify some of the things we've said earlier. If the interval between two frequencies \(a\) and \(b\) is \(x\) cents, then \(b/a = 2^{x/1200}\). Solving for \(x\) gives \(x = \frac{1200\ln(b/a)}{\ln 2}\).
In this system, every note is compromised a little compared with any "just tuning" (tuning based on the harmonic series). But, almost miraculously, none of these compromises are too severe, and overwhelmingly, at least in many musical contexts, it has been felt that the benefits of being able to play in any key, and change keys at any time without encountering any wolf intervals, is well worth the price of having every interval just a little off from what the harmonic series would have.
Let's revisit the question of why there are 12 notes in the chromatic scale. At the moment, our answer is that in the construction of Pythagorean tuning, after the 12th iteration, we begin to produce tones that are close to tones we already have. But, they are still different tones, after all, so why do we discard them so readily?
Well, let's begin by deciding, as we've done all along, that intervals of an octave of a fifth are special and desirable in our scale. We know it's not possible to stack \(k\) fifths and obtain \(m\) octaves (\((3/2)^k \neq 2^m\) for any \(k, m\)). But, though we haven't written it this way before now, we've seen that stacking 12 fifths gives approximately 7 octaves: \((3/2)^{12} \approx 2^7\).
But are there \(k, m\) which make this approximation even better?
If we take the logarithm of \((3/2)^k \approx 2^m\), we obtain \(k\ln(3/2) \approx m\ln2\), or \(m/k\approx \ln(3/2)/\ln2\). The goal is to find \(m,k\) that best approximate \(\ln(3/2)/\ln 2\) in the following sense: any better approximation must have a larger denominator. Since the denominator, \(k\), is the number of stacked fifths, this means that we do not want to stack a large number of fifths when we could get a better approximation by using fewer fifths.
Now, \(\ln(3/2)/\ln 2\) is an irrational number (this is really just a re-phrasing of the fact that \((3/2)^k\neq 2^m\), but it can be written as a continued fraction:

If we truncate the process at any time, we obtain an approximation which is called a convergent.
Here are the first few convergents:
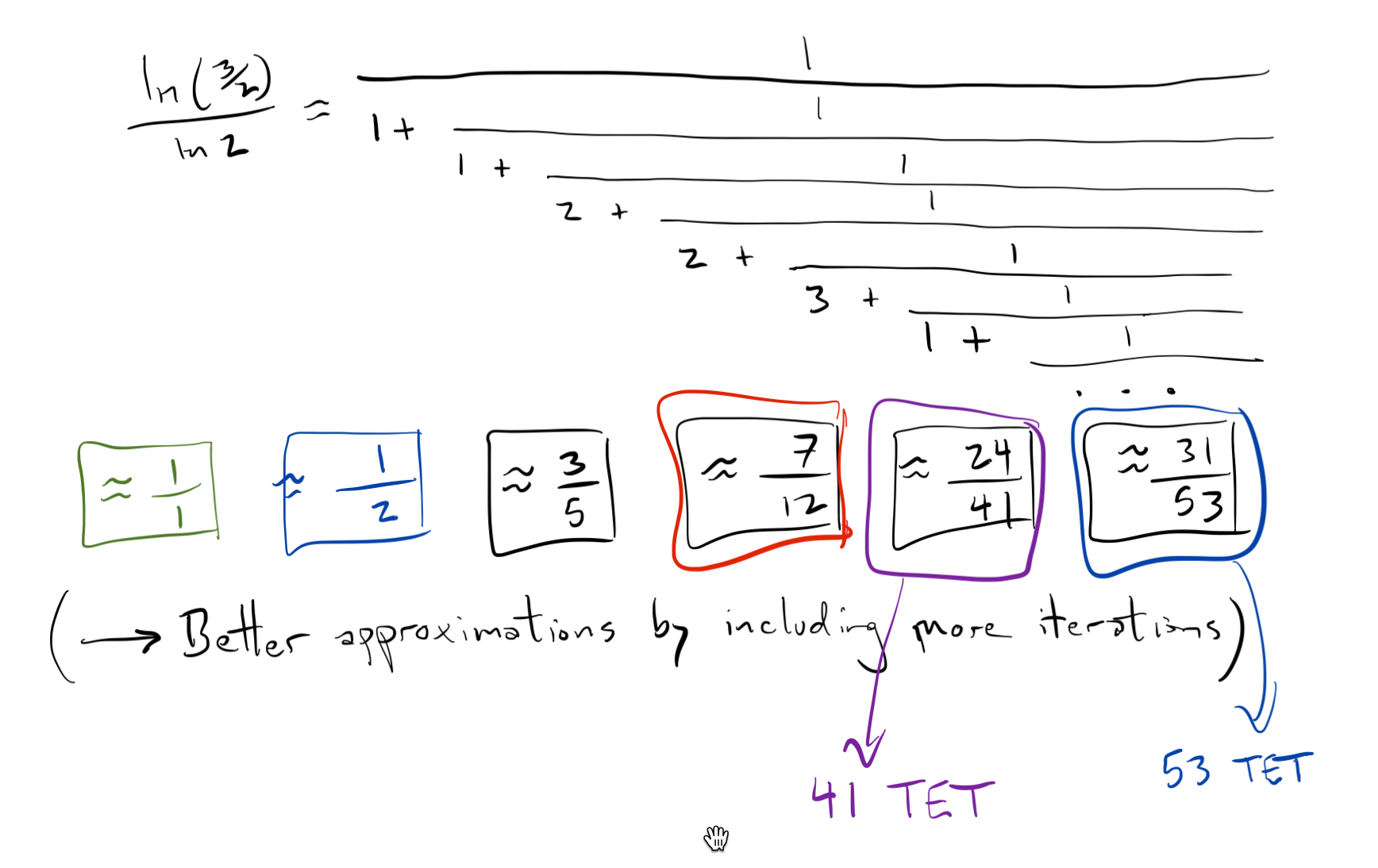
Notice that \(7/12\) is a convergent; stacking 12 fifths is approximately the same as stacking 7 octaves, as we have previously seen! If we were to continue the process of stacking fifths, we would not, in fact, get any closer to an octave until the 41st iteration; the next convergent is \(24/41\), which means stacking 41 fifths is approximately the same as stacking 24 octaves. Thus one can construct a 41 tone equal tempered scale.
The fact that \(7/12\) is a convergent that occurs fairly early on in the continued fraction expansion is another justification for why the twelve tone chromatic scale is so common.
resource link
 Sound Pressure Waves.
Black lines could represent drum head or string; dotted purple line represent pockets of air.
A dot above a particular region oscillates up and down, and its corresponding sine wave is pictured.
Sound Pressure Waves.
Black lines could represent drum head or string; dotted purple line represent pockets of air.
A dot above a particular region oscillates up and down, and its corresponding sine wave is pictured.
 Vibrating String.
Harmonics, up to tenth, in red (not pictured).
Table of scale factors for summing harmonics to create vibrating string.
Vibrating String.
Harmonics, up to tenth, in red (not pictured).
Table of scale factors for summing harmonics to create vibrating string.
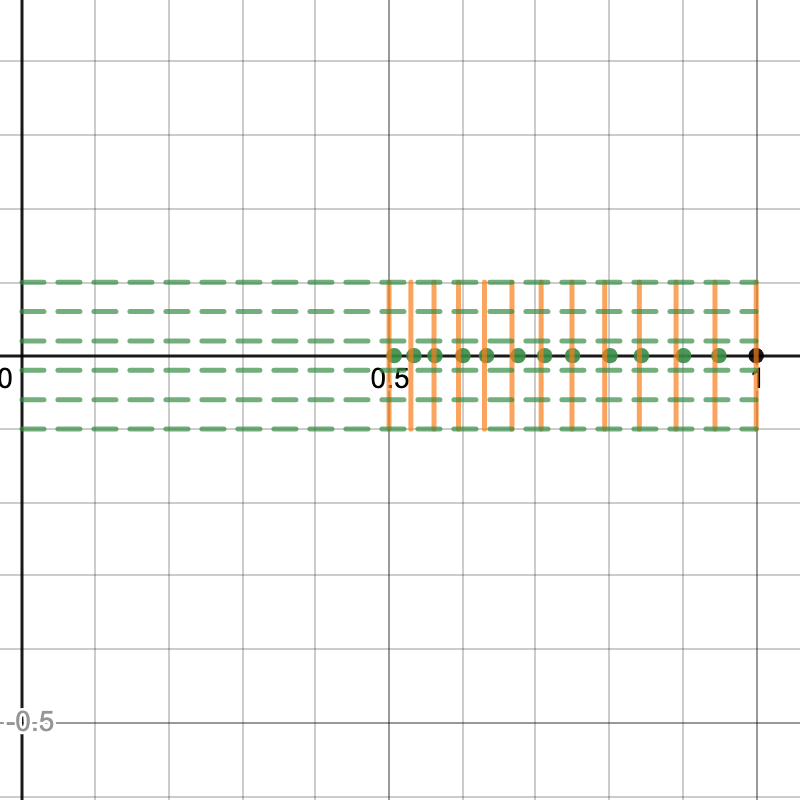 Guitar frets.
Orange lines indicate the placement of frets according to 12 TET.
Green dots indicate the placement of frets were we to obtain twelve pitches only by "stacking fifths" upwards.
Guitar frets.
Orange lines indicate the placement of frets according to 12 TET.
Green dots indicate the placement of frets were we to obtain twelve pitches only by "stacking fifths" upwards.
- Calculating frequencies, by stacking fifths up and down. Also includes overtone series. Computations are stored in arrays and lists which can be sorted.
- Equal Tempered Scale Generation
- Math of scales blog post. Very well written. Covers Pythagorean tunings, just tunings, continued fractions, etc.
- Quanta article on octave perception; Tsimane tribe.
- Relating Tuning and Timbre, article by William Sethares. Touches on synthesizers, dissonanace curves, timbres of instruments.
- David Benson's page, with a link to his textbook
- Online tone generator. Very flexible.
- Another online tone generator, not as flexible, but check out the DTMF signals.
- Collection of Java applets. Very well done; see the Fourier Series app.
- 3blue1brown on music and measure theory.
- Adam Neely on Benedetti's Puzzle, impossible music (syntonic comma, etc)
- Minute Physics; references the Rational Root theorem for why \((a/b)^n\neq 2\) for any \(a,b\).
- 12-tone on just tuning and commas
- 12-tone on the Genesis scale
- 12-tone on scales of Wendy Carlos